Financial Derivatives

When I started to work for my current company, I have struggled to get one simple overview of this universe. Instead I had to consult many sources, lot of them were going deep into details of one particular financial product. An I was not and still I am not interested in details of investment banking but just needed simple overview.

Over the time I took notes, and kept them for myself, getting information mostly from wikipedia or investopedia. I have posted it here, just in case that it might help someone in the same position that I was.

The world of derivative products is not that complicated. From my (developer's point of view) understanding the basics of derivatives is easy. The finance guys make it bit more complicated by using special vocabulary. For instance selling and option might be called "writing an option". The price of the stock at the time that the broker and the investor exchange the option might be called "Final Reference" or "Spot Price" and so on. You might also understand a product (such as future) but you might get confused by the way it is priced – that is the way that the brokers and investors agree on prices (percentage, basis points, spreads).

• Basic vocabulary and terms
• Financial instruments
• Financial derivatives
  • Options
    • Call Option
    • Put Option
    • Delta, Implied Volatility
    • Strategies
    • Options and Hedging
    • Barrier Options
    • Warrants
    • Options pricing
  • Futures and Forwards
    • Futures and Forward pricing
    • Futures and Forward rolls
  • Convertible Bonds and Reverse Convertibles
    • Convertible Bonds
    • Reverse Convertibles
  • Swaps
    • Volatility and Variance Swaps
    • Total Return Swaps
  • ETFs
    • Net Asset Value
    • Creation Redemption
  • Other Crazy Stuff
    • Autocallables
    • Program Trading

Basic vocabulary and terms

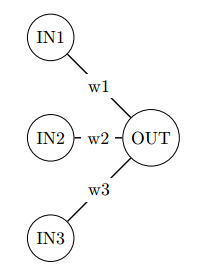
There are two entities in this business:

• Asset Manager - a company which has collected large amount of money and invests this money hoping in regular profit. Asset Manager can be also called Buy Side, because historically and probably still he buys more, but he sells as well. So a buy side can be pension fund, mutual fund a big private equity or a hedge fund – in general anyone with enough money.
• Broker - usually a bank. It is the one that gives to Asset Managers what they need. That is the access to the shares and they also create the derivative products that the buy side can use either to risk or to hedge himself while buying some shares. Brokers are called Sell Side as well, because they sell more than buy, even though, they do both (as well as Asset Managers).

Underlying - underlying is anything that you can buy. Usually shares (stocks) or commodities but in some circumstances and underlying can be also a future. The idea is that it “underlies” the derivatives product. For instance you can buy an option on stock of Google. In that case the stock of Google is the underlying. The derivatives are products that are derived from the underlying. An option gives you the right to buy the underlying at some time in the future. A forward will oblige you to buy a stock at the price that you have agreed at some point in the future. A swap will obligate to exchange the underlying for something else. You could create an agreement to swap at some point 200 shares of Google stocks for 1000 liters of beer. This kind of swap would be a derivative with 2 underlyings (shares of google and beer).

Short - means to sell, shorting something means selling that given underlying.

Long - means to buy, being long in something means to buy and underlying and keep it.

List of financial instruments

Financial instruments are anything that you can trade on the markets. Derivatives as such as one category of financial instruments but unlike the basic once, they are "made of" them.

• Equities - stocks, shares
• Debt - bonds or mortages. This products are also called Fixed Income products, because the borrower or issuer aggree on regular payments
• FX - Currencies and Rates
• Commodities - oil, gold, whatever. Not really Financial Instrument, but you can trade it and the derivatives can be based on these as well
• Derivatives - further described in this article. Products derived from all of the other once with additional conditions and rules

Financial Derivatives

This list of financial derivatives is definitely not complete and it is just a try for some logical segregation (which can be sometimes quite hard in this field)

• Options and stratgies - Options give the right to buy or sell and are a basic building block. Two or more options in the same time form strategies, which give interesting exposures.
• Forwards and Futures - the obligation to buy something in the future for fixed price.
• Convertible Bonds - enable the change of a bond into stock
• Swaps Variance, Volatility or Return Swaps - basically exchanging performance or volatility of one stock for other stock's
• ETFs - Exchange-Traded Fund. Can be seen as a stock composed of other stocks
• Others: Autocallables, Accumulators, Program Trading and many other magic stuff

Options

There are two basic types of Options: CALL which gives the owner the right to buy and PUT giving the owner the right to sell. These two basic types can then be composed to form a "strategy". Strategy is just a fancy world used for buying or selling two options at the same time. As you can see later one can choose to do that for multiple reasons.

Call Option

Call is the right, but not the obligation to buy given underlying (stock or commodity) at given price until given date.

A trader who believes that stock's price will increase can buy the right to purchase the stock (he buys call option) at a fixed price, rather than just purchase the stock itself. He would have no obligation to buy the stock, only the right to do so until the expiration date. The price that he will pay for that option is called Premium. If the stock price at expiration (also called Spot Price) is above the agreed price (also called Strike) by more than the premium paid, he will profit i.e. if S>X, the deal is profitable. If the stock price at expiration is lower than the exercise price, he will let the call contract expire worthless, and only lose the amount of the premium. The option is less expensive than the shares itself. For less money the trader can control larger number of shares. That is why we talk about leverage.

Options parameters:

• Premium - the priced paid for the option
• Strike - the agreed price at which the underlying will be bought
• Expiry date (maturity) - the date at which the option expiries (until when you can use it)
• Settlement- either the real underlying is exchanged at expiration date ("Physical") or money is exchanged in place of the underlying ("Cash").

To visualize the options and other derivatives one can use the pay-off charts. On the X-axes of the charts we have the price of the underlying (commodity or stock) and on the Y-axes we have the total profit.

Put option

Put option gives the owner the right to sell the stock for given strike price, otherwise all other parameters are the same.

A trader who believes that a stock's price will decrease can buy the right to sell the stock at Strike price. He will be under no obligation to sell the stock, but has the right to do so until the expiration date. Logically the one who sold him the option will have buy the stock from him (if at some point the option will really get used) If the stock price at expiration is below the exercise price by more than the premium paid, he will profit. If the stock price at expiration is above the exercise price, he will let the put contract expire worthless and only lose the premium paid. Again here are the 2 pay off chats. If you bought a PUT for a MSFT stock with strike 100 for 10 dollars, you bought yourself the right to sell MSFT stock for 100 dollars. Now if the price is 90, you didn't lose anything but did not get anything either. On the other hand if the price did not move and it is still 100, you lost your 10 dollars. That shall be clear from the pay-off chart.

One has to understand, one the market one can buy or sell both types CALLs and PUTs. The outcome of each operation is different. The following chart, shows all 4 operations that can be done.

Delta and Implied Volatility

Delta always and implied volatility sometimes are parameters that the brokers provide with the price of the option, when they want to sell you one.

Delta expresses in percent the change in the price of the option with respect to change in price of the underlying. That is how much will the option price change if the underlying stock moves up or down. Delta is one of the so called Greeks that are briefly discussed later. Delta is expressed in percentage. If a stock costs 10$ and an option (with some maturity) is selled for 5 dollars and the Delta of the option is 50%, then if the stock goes to 11$, the option will go to 5.5%. That is called a delta adjustment. The broker at some point proposes a price to the investor and provides the delta as well. If the investor buys in next hour, he knows what the price of the option will be at the deal time.

Delta is always positive for a CALL and negative for a PUT. If a price of the underlying goes down, then the price you pay for the right to sell such share on some fixed price goes up. If the price of the underlying falls from 10 to 1, and you had an option giving you the right to sell for 5, you are lucky since, since you will be selling much above the market. It's clear that price of such option goes up. The reverse is true for the call. If the price of the underlying goes from 10 to 15, and you wanted to buy an option with strike 12. The broker was willing to sell you such option for 11 before, but it's price went definitely up.

Implied Volatility is another parameter sometimes provided by the brokers when giving the prices. In order to provide the price for any given option, the broker estimates the volatility of the market in the future. Implied Volatility is such estimation. Options are priced by using different variations of Black Sholes furmula. The basic idea behind this formula states, that the price of an option does depend only on it's parameters, current price of the option and the estimated volatility of the market. Of course when a broker gives a price of an option, the price will depend also on other factors, such as whether the broker has any shares of the given underlying already. But in theory, the broker could just provide the estimated volatility that he puts into his model and that is enought to calculate the price.

Options trading and hedging against delta adjustment

When a trader wants to obtain an option, he will specify the parameters and ask brokers whether they can give him such contract. The broker will give to the trader the price for such contract and also the delta. That is the rate at which the contract price will change with respect to the change in the underlying.

If the contract is big enough, the broker might need some time to acquire enough shares. Also the buyer might take some time to decide whether to buy or not. So after all this delay, the price of the option contract has changed by delta*(underlying price change). The buyer might have lost money.

To evict such situation, options hedging is used. In this situation, the broker will buy from the buyer of the option such amount of shares of the given underlying, so the change of the price of the option contract will be completely mitigated by this operation.

Strategies based on options

Calls and Puts can be bought or selled in the same time with diferent parameters. This results in diferent pay-offs of such operations. Buying or selling multiple options at the same time in the same contract is called buying a "Strategy". Here is probably non-complete list of strategies:

• Call spread and Put Spread
• Strangle
• Straddle
• Butterfly
• Risk Reversal
• Collar
• Condor
• Box Option

Call spread

This strategy consists of two calls with the same expiry. The first one with smaller strike is sold and other with higher strike is bought.

The payoff is shown bellow. Call spread behaves liked to underlying, but the maximum profit and maximum loss values are limited by the strike prices of the calls.

Analogically to call spread, put spread is a strategy composed of two put options, with the same expiries and different strikes.

Strangle

Strangle allows the holder to profit based on how much the price of the underlying security moves, with relatively minimal exposure to the direction of price movement. Long stangle is composed of long call and long put, with same expiries. The profit potential is unlimited, the strategy may be used in volatile markets.

Short strangle is composed of short put and short call with same expiries and it is profitable if the price of the underlying does not move much and the profit is limitted to the premiums obtained, otherwise the potential loss is unlimited.

Straddle

Very similar to strangle, Long Straddle is a long call with a long put, with same strikes and expiries.

Strategy involving the purchase or sale of particular option derivatives that allows the holder to profit based on how much the price of the underlying security moves, regardless of the direction of price movement. Long straddle = long call option + long put option – same strike and expiry. As for strangle, this strategy might be usefull in highly volatile markets.

Again Short straddle is like short strangle, but strike is the same. The price has to stay very close to the strike for a profit based on premiums.

Butterfly

Limited risk, non-directional options strategy that is designed to have a large probability of earning a limited profit when the future volatility of the underlying asset is expected to be lower than the implied volatility.

Risk reversal

Selling an out of money put and buy out of money call with same maturity. An investor wants to go long in the underlying but instead of going long on the stock, he will buy an out of the money call option, and simultaneously sell an out of the money put option. Presumably he will use the money from the sale of the put option to purchase the call option. Then as the stock goes up in price, the call option will be worth more, and the put option will be worth less. If an investor holds the underlying and sells a risk reversal, then he has a collar position.

The pay-off is exactly the same us holding the underlying stock. One could use risk reversal to speculate on a stock without holding the stock.

Collar

• Long the underlying
• Long a put option at strike price X (called the "floor")
• Short a call option at strike price (X+a) (called the "cap")

Latter two are a short Risk reversal position,so we can say Underlying - Risk reversal = Collar. The profit or loss on underlying are very limited.

The premium income from selling the call reduces the cost of purchasing the put.

Condor

Stragy with limited risk, non-directional (the same result if underlying moves either way) with limited profit when the underlying security is perceived to have little volatility.

• Sell 1 In The Money Call
• Buy 1 In The Money Call (Lower Strike)
• Sell 1 Out of The Money CALL
• Buy 1 Out of The Money CALL (Higher Strike)

Maximum profit for the long condor option strategy is achieved when the stock price falls between the 2 middle strikes at expiration. It can be derived that the maximum profit is equal to the difference in strike prices of the 2 lower striking calls less the initial debit taken to enter the trade.

Box option

Combination of 4 basic legs, that achieves neutral interest rate position - riskless payoff.

• Long call strike 10
• Short call strike 15
• Long put strike 15
• Short put strike 10

The strategy has constant payoff, in ideal case the net premium paid for the strategy should be equal to the payoff. However the comission will reduce the profitability to nothing. Might be seen as a form of lending money on markets.

Barrier options

TODO!!!

Warrants

Warrants have the same parameters and behave just like options. There are few differences:

• They are not publicly traded, not listed, like OTC options.
• The expiration period is usually in years.
• Once the warrant is exercised the new outstanding shares of company are created. In case of options, no new shares are issued, the writer of the option has to buy them on the market.
• Often used as alternative to employees stock options.

Specifying option and it's price

This part is not about the actual pricing of options, that is determining the price. This is more about how options are exchanged on the market, in what units the prices as exchanged.

• Fixed price per contract
• In percentage
• Spread between legs
• Pricing by strike
• Total premium for multilegs

Forwards & Futures

By buying a forward or future, you have the right but also the obligation to buy given underlying at the selected price. Both are part of Delta One products. Since the price of the future moves the same way as the price of the underlying. Futeres unlikely to forwards are listed, standardized contracts. That means they can be bought on an exchange. Forwards are pure OTC products - not standardized at all.

Futures or Forwards have the same parameters as options, though in the majority of cases, no strike is specified. That is because the price at which the underlying will be exchanged at the expiration date, is defined solely by the market. Typically futures prices are listed on the market. For instance the current price of SPX Indice might be 2000 and the future which expires next month might be at 2050.

Pricing of futures

Futures are delta-one derivatives. The price of the future changes hand in hand with the price of the underlying (if the stock goes up one dolar, the future on the same stock in 3 months will go up as well by one dollar). That affects the way that futures are priced. Since typically the future price is always specicied with respect to the current stock price, there are 2 common ways of pricing futures:

TODO!!!

• Net Basis - the difference between stock price and future price is given by the broker in basis points.
• In Percentage - the future price is given as the percentage of current price. For bullish stock that will be greater than 100% and for bearish stocks that will be lower than 100%.

Future and Forward Rolls

Rolls enable the holder of given future to keep the position in the underlying when his future is about to expire.

Convertible Bonds, Reverse Convertible Bonds

These two derivatives at some point allow or force the holder to convert bonds into shares.

Convertible Bonds

Convertible Bond is a contract which allows the conversion of listed corporate bonds into the underlying equity. This is available only on listed companies that issue as well bonds to finance their operations. Converts are listed on exchanges. The companies issue the CBs just like the bonds the are underlying the converts.

From certain point of view, CB can be seen as an option, because if underlying stock behaves achieves certain performance, the owner will become the proprietary of the stock, if not, he will keep the bonds with regular return. For that reason, it makes sense to provide Delta while pricing Convertible Bonds, since the price of the CB will move with respect to the underlying share.

Convertible bond thus has the power of option and can be leveraged to obtain the underlying equity. It will be however more expensive than CALL option becase one pays for the bond as well.

Reverse Convertibles

Holder of a Reverse convertible is regulary paid a coupon as if he would be holding a standard bond. On the upside if the shares of the underlying company (and that can be any company, not just the issuer of the original bonds) fall bellow certain PUT like Strike. His bonds will convert into the stocks of this company

Swaps

Swaps as the name suggest are contracts that specify an exchange between the buyer and the seller of the contract. There are various types, depending on what is exchanged: Commodity, Interest Rate, Volatility or Variance.

Variance and Volatility Swaps

Volatility measures the magnitude of movements for given stock. Standard deviation is used to express the volatility of the stock. Variance is the square of standard deviation, so in a sense just amplified volatility.

Volatility or Variance swap allow the investor to bet on the volatility. The investor specifies a volatility level which he expects (striked volatility) and if the volatility goes over this level, he gets paid a bigger payoff. The payoff is specified as:

PayOff = VegaAmount (RealVolatility – Volatility Striked)/ RealVolatility

The bigger the difference between the Real Volatility and the Striked volatility is, more money does the buyer of such swap gets. The whole amount is multiplied by a multiplier called "Vega Amount". Vega is on of the greeks which meassures the sensitivity of an option to the change in the volatility of the option. There is however no connection here. It's just the term used on the markets for this multiplier.

Total Return Swaps

TRS allows the buyer to exchange the performance of certain stock for the performance of standard interest rate. The buyer can for instance bet on the performance of certain underlying (eg. MSFT stock) against a standard interest rate for standard period. For instance Euribor 6M is the interest rate provided by ECB (European Central Bank) for next 6M. That might be 2% fo example. The buyer believes that MSFT will beat that and asks the seller to pay him the difference if that is the case. The seller, for certain comission will do that. That allows the asset manager to bet on performance without owning the underlying shares.

ETFs

Exchange Traded Funds are compositions of stocks, that usually track an index or a sector. They are listed and traded like regular stocks. They companies that emit ETFs thus enable the asset managers to invest into whole sectors or regions, without the need of knowing the details of the markets.

Net Asset Value

Common to all funds which invest into stocks. At the end of the day the NAV of the fund is calculated as the sum of all the stocks own by the fund, divided by the number of shares.

ETFs however are listed themselves and traded on the market so beside the NAV they also have the market value. Their market value can be bellow or over the NAV.

Settlement date

The date when you need to the money to buy your ETF or when you will receive the money for selling. For ETFs it is 3 days after the deal (for some traditional reasons, I suppose).

Creation Redemption

Creation is the process of emission of ETF shares. ETF is supposed to track a sector or index and has exact composition. The company issuing ETFs needs to aquire the stocks that form the ETF to emit it. Since one share of ETF has exact composition, the issuer needs to aquire that exact amount to be able to sell that one share of ETF with certain comission.

Redemption is the reverse process. The issuer will buy the ETFs from the owners and give them back the underlying shares, or equal amount in cash.

This process is essential and allows the ETF to always trade around it's NAV. If the demand fo some ETFs (eg. ETF mirroring Asian construction market) would be too high, the prices would go up too much and get too far away from the real prices of the shares of the mirrored companies. The issuer can in that case emit more shares of the ETF. On the other hand if investors start to sell certain ETF too much and don't believe in the sector, the redemption process can reduce the quantity of the ETFs and stabilize the price which would go down too much otherwise.

Other crazy stuff

Autocallables

TODO!!!

Program Trading

An asset manager might interested in investing in sectors or countries, not exact shares. ETFs are one way to get there, Program Trading might be the other way. PT are basket trades (buying multiple underlyings in same time) and are very big in size, the buyer specifies the total amount of the traded volume (total notional) and might provide also the number of stock he wants to buy in the future. Then he gives multiple characteristics such as the percentage per country or sector. For instance 10% in US, 30% in UK and 25% in Telecom, 50% in services and so own. He also asks certain parameters such as how much this composition should track some index. This is done usually by setting the Beta in percent versus some index like SPX. The seller of such contract than provides price and some (huge) commission.

The investor will do such a trade when he wants to invest big amount of money in the same time to multiple markets. Usually the trade composition is determined by dedicated software, hence "Program Trading".

Neural Networks F#, XOR classifier and TSP Hopfield solver

It seems that recently thanks to the buzz around Deep Learning, Neural Networks are getting back the attention that they once had. This post contains just a very short introduction to Neural Networks, just enough to understand the F# code which follows. The aim for me is to learn F# and see how easy it can be to write Machine Learning code in F#.

I present here two examples of NN in F#:

• XOR classifier - sort of Hello World of NN. A simple composition of 2 input nodes, 2 hidden nodes and 1 output node which learns the XOR function.
• Solution to TSP using Hopfield NN. More complex network which evolves over time in it's configuration space to it's local minima, which shall correspond to optimal TSP tour.

Both working examples are available at my GitHub

Neural Networks

Artificial neural networks are computational models with particular properties such as the ability to adapt or learn, to generalise or to cluster and organise data. These models are inspired by the way that the human brain works. The building blocks of Neural Networks are inspired by Neurons - the building blocks of our brain. Neural Network can be seen as interconnected graph of nodes, where each node takes a role of a neuron. Each neuron can receive multiple signals, modify it and send it to other neurons to which it is connected. In this graph some vertexes are used to set the input, some of them are used to perform the computation and other onces will hold the output values.

Nodes are connected by edges which have different weights. The weight of the edge specifies how the signals is modified when passing from one node to another.

Perceptron

Perceptron is a basic block of linear neural networks. It is composed of multiple input nodes and a decision node. Perceptron is a single layer network. Input values are linked directly to the output node, connected by edges with certain weights.

The ouput node takes the incomming values, sums them and based on the result returns an output. The output could be binary or continous value. For instance a threashold can be used to say whether the output is 1 or 0.

In practice, very often the Sigmoid or also called logistic function is used to output value within the interval [0,1].

Linear separability

Single layer perceptrons can only learn linerearly separable data.

Imagine we want to separate a set of datapoints into multiple clusters. We visualize the data in 2-dimensional euclidian space. If we can separate the cluster by drawing direct line between the data points, the data is linearly seperable. The same can be applied on multi-dimensional data

In a world of logical functions (we are building XOR classifier), this limitation means that a single layer perceptron is able to learn AND or OR function but it won't be able to learn XOR function.

One can easily imagine a line that separates all OR positive results from the negatives once. On the other hand there is no streight line that separates the positive XOR results ([0,1] and [1,0]) from the negatives ([0,0] and [1,1])

Feed forward multilayer networks

Feed forward network can be thought as composition of perceptrons. Such network has one input layer, multiple hidden layers and one output layer. The feed forward network does not contain cycles, unlike the Hopfield network in the next examples (which is recurrent neural network).

Unlike single layer perceptron, multilayer feed forward network is capable of learning linerably non-separable data such as the results of XOR function.

XOR classifier

This is the first example. This network is called clasifier because it learns the XOR function. It can then "classify" the 2 values in the input into single value on the output.

Here is how the network looks like:

The NN diagram was drawn in latex, using the tkz-berge package. Look here if you want to know how.

The network starts with random weights and continously updates the weights so that the result in the output node corresponds to the XOR of input values. In order to update the weights Backpropagation (Backwards propagation of errors) technique is used.

The value of the output is compared to the real value (which is known). The error is determined as the differences between the output and the real value. Then the weights of the edges has to be updated to minimalize the error as shown later.

Implementation

Each layer can be represented as one dimensional array, the weights are stored using 2-dimensional array ([0,1] is the weight between nodes 0 and 1). Here is the function which calculates the sum of values incomming to a single node and passes the value to the activation function. The activation function here can be any function, as it is passed as parameter but here Sigmoid is used.

let pass (input:float[]) (weights:float[,]) activation =
let length = weights |> Array2D.length2
seq {
    for i in 0 .. length-1 do
        let sum = (Array.zip weights.[*,i] input) |> Array.sumBy (fun (v,w) -> v * w)
        yield activation sum
} |> Array.ofSeq

By applying the pass multiple times, the whole network can be composed as sequence of pass functions.

The training procedure

The following function is the main loop of the XOR network and we iterate over until we obtain good results and the network is adapted.

let train network rate input target =
    let n1 = completepass input network
    let delta = deltaOutput n1.output target
    let deltaHidden = passDelta n1.hidden delta n1.hiddenToOutput
    let updatedHiddenToOut = updateWeights n1.hidden delta n1.hiddenToOutput rate
    let updatedInToHidden = updateWeights n1.input deltaHidden n1.inputToHidden rate

Completepass just calls 2 times the pass function value and gets the input values trough the hidden layer to the output. The output is then compared to desired result and error is estimated. From this error an array of "delta" values per each output node is determined which is then used to update the weights.

In the case of XOR network, there is only one output, so the delta will one dimensional array.

The delta has to be propagated lower so that we can also update the weights between the input and hidden layer.

Backpropagating the error

First the error of each layer has to be calculated. In the example bellow the error of the output layer is the value (t-o) or (Target - Ouput). This value is multiplied by value o*(1-o) which is the derivation of the Sigmoid function. The resulting array contains for each node a delta value, which shall be used to adjust the weights.

let deltaOutput (output:array<float>) (target:array<float>) =
 (Array.zip output target) |> Array.map (fun (o,t) -> o * (1.0 - o) * (t - o))

Delta propagation

Calculating the delta value for the output layer is not sufficient to correct all the weights in the network, the delta has to be propagated to the lower layers of the network, so that we can update the weights on the input - hidden connections.

let passDelta (outputs:float[]) (delta:float[]) (weights:float[,]) =
    let length = weights |> Array2D.length1
    seq {
        for i in 0 .. length-1 do
            let error = (Array.zip weights.[i,*] delta) |> Array.sumBy (fun (v,w) -> v * w)
            yield outputs.[i] * (1.0 - outputs.[i]) * error
    } |> Array.ofSeq

The "error" of the hidden layer is just the delta multiplied by the weight associated to the edge that propagates this delta to the lower value.

The last missing piece is the function that woudl update weights between 2 layers.

let updateWeights (layer:float[]) (delta:float[]) (weights:float[,]) learningRate =
    weights |> Array2D.mapi (fun i j w -> w + learningRate * delta.[j] * layer.[i])

Learning rate is a constant that determines how quickly the edges are updated. If the learning rate is too big, the network might miss the optimal weights. However if it is too small it will take longer time to get to the correct solution.

At the beginning the weight are set to random values between 0 and 1, or slided slightly. From the quick tests that I did it seems that for instance using learning rate of 0.3 it took 20000 iterations to get to a neural network that would XOR the values on it's inputs.

Hopfield-Tank network and Travelling Salesman Problem

TSP is one of the well known Combinatorial optimization problems and as such, it has been solved in many different ways (Integer Linear Programming, Genetic or Biologically inspired algorithms and other heuristics). Neural Networks are one of the many approaches to provide a solution to this problem.

Even within Neural Networks several different approaches have been developed to solve TSP (eg. elastic nets,self-organizing map). The approach demonstrated here is the oldest one: Hopfield neural network.

Hopfield neural network

Hopfield NN is a recurrent neural network (connections in the network form cycles). The units (nodes) in a Hopfield network can have only 2 values: 0|1 or -1|1 depending on literature, but in either case values that encode a binary state. The network is fully connected (each node is connected with any other node). The connection matrix is symetric, that is the weights on the edges are the same in both directions.

The initial Hopfied network had only binary values (0/1) but to solve TSP and for other problems continous version of the network is used, where every node has value in range [0,1].

The value of each node depends on the input potential of the node (Ui) and in order to keep it between (0,1) the tanh function is used:

The value of the input potential of each node depends on the values of all nodes that are connected to it and the values of the connections weights. This is actually identical to the way that the nodes in the XOR classifier behaved.

Network energy

Each state of the HNN can be described by a single value called Energy. While iterating and changing the state, the energy of HNN will either stay the same or will get smaller. The energy of the network will evenutelly convert to a local minimum - the state of the HNN that we target to solve the TSP

Hopfiled approach to TSP

The first and original approach to solve TSP was described in 1985 by Tank and Hopfield in their paper "Neural Computation of Decisions in Optimization Problems". Since then many more attempts were made. I have found these few papers or surweys available online quite useful and have used them to deduce my implementation:

• Jean-Yves Potvin - The Traveling Salesman Problem: A Neural Network Perspective
• Perspective of a neural optical solution of the Traveling Salesman optimization Problem
• Jacek Mandziuk -Solving the Travelling Salesman Problem with a Hopfield - type neural network

If I should pick one, I would say that the first one gave me most information about the problem, event though not enough implementation details. The others once then made it (almost) clear how to implement the solution.

Encoding TSP in Hopfield network

The neural network used to encode the TSP and it's solution is square matrix of nodes having N rows (one for each city) and N columns (one for each position in the tour), where N is the number of cities. When the algorithm finishes and the network converges to it's final state, each node will have value of either 0 or 1. As said the network in fully inter-connected so there is an edges between each node, which is not shown in the image bellow.

If the node in i-th row and j-th column has value 1, the city (i) will be in the tour on position (j).

As described above the network evolves and each node changes it's value over time. The secret of the algorithm is thus to provide such update rule that at the end the matrix of nodes will follow these criteria:

• Only one node in each row will have value 1
• Only one node in each column will have value 1
• There will be exactly N nodes having value 1
• The distances of the tour will be minimal

To come up with such update rule, Energy function has to be determine which will attain it's minimum for optimal solution of TSP. The energy function has to take into account the above specified rules. The following definition will satisfy the rules. Note that the following equations were taken from the J.Y Potvin's - paper

A,B,C and D are constants and the 4 sumations here correspond to the 4 above mentioned points.

Describing the dynamic of the network

There are two ways to describe the behaviour and the dynamic of the network:

• From the TSP energy function and the standard Hopfield network energy function we determine the weights between the nodes. Then we can let the network evolve over time. Since we have the weights of the connections between the nodes, we could iterate over the nodes, sum all the weighted inputs and set the output of the node. That would be an approach similar to the one taken on the XOR. This has one disadvantage, that is that the connection weights have to be determined from the equality between the standard Hopfield model enery function and the TSP Hopfield model function. There is an easier way without determining the connections weights.
• The easier way is to describe the change of the input potential without determining the weights of the edges. Then we can just iterate or randomly choose nodes, determine the new value of the potential and update the values of the connected nodes. This seems maybe ackward, because the network will evolve without having specific weighed connections between nodes. This options is described further.

The change in the node's input potential

One of the definition of the input potential of a node (i) can be described by:

What we want to determine, is how this value will change over time, when the network evolves. The change of the potential over time is it's partial derivation with respect to the time.

When doing a computer simulation we will described the value of Ui in time T+1, or here T+ delta t. Where delta T is some small time interval.

This equation is at the hearth of this algorithm. We now have an exact specification of what the value of potential Ui will be in time T+1. That is our iterating algorithm has to perfrom exactly this updated.

Implementation details

• Compute the distance matrix, containing the distance between each 2 cities
• Initialize the network with random values
• Pick randomly a node, compute the change in the input potential
• Update the value of the node from the input potential change
• Every n-iterations calculate the energy of the network
• Once the energy of the network stabilizes or you have reached fixed number of iterations - stop the process
• Translate the network into a city path

The network can be stored in 2-dimensional matrix. One can choose between storing the input potential of each node or the value of the each node, because the value of the node can be calculated from the potential at any time. I have chosen the second option and I store the input potential two dimensional array u.

The following code is the calculation of the input potential change of single node at coordinates (city,position). This is just retranscription of the equation above.

let singlePass (distances:float[,]) (u:float[,]) pms city position = 
    let n = Array2D.length2 u
    
    let values = u |> toValues pms

    let aSum = sumAllBut position (values |> rowi city)

    let bSum = sumAllBut city (values |> coli position)
            
    let cSum = (values |> Seq.cast<float> |> Seq.sum) - float(n+1)

    let dSum = dSumCalc distances city position values

    let dudt = -pms.A*aSum - pms.B*bSum - pms.C*cSum - pms.D*dSum
    //value of input potential in t+ delta_t
    let r = u.[city,position] + pms.dTime*(-u.[city,position] + dudt)
 //Alternatively according to the paper by Jacek Mandziuk one can just use the update value
 //let r = dudt
    r

There are few things to note. This code takes the distances matrix, the current state of the network (the value of input potential of each node), parameters of the network (constants A,B,C,D from equations above) and row (city) and the column (position) of the node that we are updating. The toValues method takes the current value of each node potential and returns a matrix of node values. The rowi and coli method return respecively one row or one column from 2 dimensional array. The sumAllBut method adds all elements of one-dimensional array except an element at position which is passed to the method. The dSumCalc method is the only one with a bit more compexity and it calculates the D value of the equation above (the one that assures the minimalization of the TSP circuit)

let rowi row (network:float[,]) = 
    network.[row,*] |> Array.mapi (fun j e -> (e,j))

let coli col (network:float[,]) = 
    network.[*,col] |> Array.mapi (fun j e -> (e,j))

let sumAllBut (i:int) (values:(float*int)[]) = 
    Array.fold (fun acc (e,j) -> if i<>j then acc + e else acc) 0.0 values

let dSumCalc distances city position (v:float[,]) = 
    let n = v |> Array2D.length1
    (distances |> rowi city) |> Array.sumBy (fun (e,i) -> 
        let index1 = (n+position+1) % n
        let index2  = (n+position-1) % n
        e*(v.[i,index1] + v.[i,index2])
    )

let toValues (pms:HopfieldTspParams) u = 
    u|> Array2D.map (fun (ui) -> v ui pms)

//calculates the value of node from input potential
let v (ui:float) (parameters:HopfieldTspParams) = (1.0 + tanh(ui*parameters.alfa))/2.0

The method which updates the input potential of single node can be called in 2 different ways. Either we pick the nodes randomly multiple times or we loop over all the nodes serially. If the update is serial then the only random element of the algorithm is the initialization of the netwok.

let serialIteration u pms distances = 
    u |> Array2D.mapi (fun i j x -> singlePass distances u pms i j)

let randomIteration u pms distances = 
    let r = new Random(DateTime.Now.Millisecond)
    let n = Array2D.length1 u
    for i in 0 .. 1000*n do
        let city = r.Next(n)
        let position = r.Next(n)
        u.[city, position] <- singlePass distances u pms city position
    u

The random iteration here is repeated 1000*n times where n is the number of cities, which is probably more than enough since the network seems to converge much sooner. Just for the sake of completeness, here is the method that runs 10 times either serial or random iteration.

let initAndRunUntilStable cities pms distances = 
    let u = initialize cities pms
    {1 .. 10} |> Seq.fold (fun uNext i -> 
            match pms.Update with
                | Random -> randomIteration uNext pms distances
                | Serial -> serialIteration uNext pms distances
    ) u

And here high level method, that generates a random example of TSP problem, calculates distances between all cities and runs the algorithm until a stable and correct solution is found. That is until the network returns feasable solution.

let sampleRun (pms:HopfieldTspParams ) (n:int) =
    let cities = generateRandomCities n
    let distances = calculateDistances cities
    let networks = Seq.initInfinite (fun i -> initAndRunUntilStable cities pms distances)
    let paths = networks |> Seq.map (fun v-> currentPath v)
    let validPath = paths |> Seq.find (fun path -> isFeasable path)
    cities, validPath

Results

The results are not overwhelming, on the other hand I have only implemented the most simple version of the algorithm. In the original paper the authors stated that the convergence rate to feasable solutions was about 50%. But depending on the parameters one can get better results. See bellow one of the runs of the algorithm on 6 random nodes.

Here is the complete list of parameters for Hopfield network and the values that I ended up using:

• Alpha: the parameters which shapes the Sigmoid decision function applied on each node (500)
• A: input potential change function, sum of rows (500)
• B: input potential change function, sum of columns (500)
• C: input potential change function, max N cities (200)
• D: input potential change function, minimalization of tour length (300)
• dTime: represents the delta T, the small update in time for each update of the input potential value (0.00001)

I have also used the standard update rule to obtain new value of the input potential which takes into account the current input potential.

     let dudt = -pms.A*aSum - pms.B*bSum - pms.C*cSum - pms.D*dSum
    //value of input potential in t+ delta_t
    u.[city,position] = u.[city,position] + pms.dTime*(-u.[city,position] + dudt)

According to the paper by Jacek Mandziuk one can just use the updated values as the new input potential, so that the update rule would become only:

    let dudt = -pms.A*aSum - pms.B*bSum - pms.C*cSum - pms.D*dSum
    u.[city,position] = dudt;

This rule didn't work for me. The convergance rate wasn't better neither were the tours lengths. Of course for such version, different values for network parameters have to be used.

Note that GitHub repostity and specifialy the Hopfield module contais more code:

• Method to determine the correct parameters. The performance of the algorithm greatly depends on the parameters of the Energy function and on the parameter alfa, which amplyfies the effect of the input potential on the value of given node.
• Few lines are also available to draw the solution using Windows Forms Charts, through F#

FSharp.Data and Unit Testing issues

I have recently run into two separate issues while testing some F# data providers based code. I am using ReSharper's NUnit runner and sometimes NCrunch.

NCrunch issues

NCrunch won't compile your solution when FSharp.Data is referenced. This component internally references FSharp.Data.DesignTime which has to be avaiable for the compilation - and NCrunch does not have those libs available, because the DLL is not referenced the standard way, but must be provided by Visual Studio.

The current solution is to reference FSharp.Data.DesignTime manually. If you are using nuget, than the DLL can be found in the pacakages foder as shown bellow:

Note that I have tested and had the same issue with FSharp.Data 2.1.0 and 2.2.0.

NUnit runner issues

NUnit did load the test correctly, but the test failed with SystemMissingMethodException

Luckily the solution can be found on StackOverflow and was caused by the tested library being Portable Class Library instead of standard F# library.